Twice recently I’ve wanted to check the proportional coverage of a dataset. For example, I have a dataset where trees are nested within plots. I wanted to check what proportion of trees within each plot had measurements in the TRY global trait database for leaf nitrogen per dry mass. Specifically, I wanted to check what proportion of plots had at least a given proportion of trees or more represented in TRY.
I could have visualised this with a histogram, but it’s not very visually appealing because it requires some mental gymnastics to add up each bin greater than the minimum threshold:
A better method I’ve found is an Empirical Cumulative Density Function (ECDF) plot.
First I have the dataframe, where each row is a tree, with plot ID, species, and mean leaf nitrogen per dry mass for that species. If a species doesn’t have a nitrogen measurement, it’s recorded as NA:
| plot | species | leaf_n |
|---|---|---|
| JLG_10 | Combretum collinum | 24.29 |
| JLG_10 | Pericopsis angolensis | NA |
| JLG_10 | Pericopsis angolensis | NA |
| JLG_10 | Burkea africana | 20.72 |
| JLG_10 | Burkea africana | 20.72 |
| JLG_10 | Burkea africana | 20.72 |
Then I calculate the proportion of trees with trait measurements:
# Split stems data by plot
dat_split <- split(dat, dat$plot)
# For each plot, proportion of trees and ba represented for each trait
prop <- do.call(rbind, lapply(dat_split, function(x) {
n_trees <- nrow(x)
data.frame(
plot = unique(x$plot),
n_trees,
prop_leaf_n = nrow(x[!is.na(x$leaf_n),]) / n_trees
)
}))
Then calculate what percentage of plots have above a minimum threshold of trees with measurements:
thresh <- 0.8
prop_plots <- sum(prop$prop_leaf_n > thresh) / nrow(prop)
Then I can make an ECDF plot using {ggplot2}:
ggplot() +
geom_line(data = prop,
aes(x = prop_leaf_n, y = 1 - ..y..),
stat = "ecdf", pad = FALSE) +
geom_vline(xintercept = thresh, linetype = 2, colour = "red") +
geom_hline(yintercept = prop_plots, linetype = 2, colour = "red") +
labs(x = "Proportion of trees", y = "Proportion of plots") +
theme_bw()
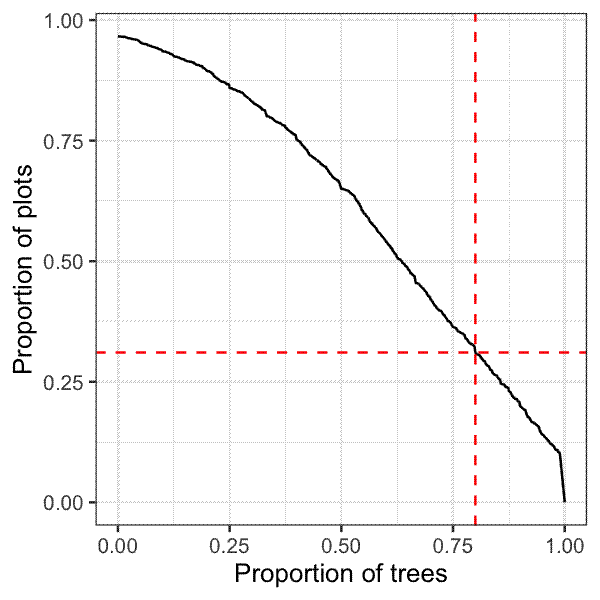
From the plot above it’s easy to see that in 31% of the plots at least 80% of trees have at least one leaf nitrogen measurement in the TRY database. It’s also easy to see the trend in the coverage. Hardly any plots have all trees covered by leaf nitrogen measurements, and it really drops off a cliff at about 98% tree coverage.
The plot above is generated from a real dataset of ~1250 woodland/savanna plots in southern Africa. It’s easy to see that trait coverage is not great in southern African species, especially given that leaf nitrogen is one of the most commonly collected traits that can tell us a lot about life history strategy and place am individual on the leaf economic spectrum. When you aggregate to genus coverage gets a bit better, but I am sceptical about how much I can trust a trait estimate that is an aggregate of species potentially found across the world. Additionally, these graphs only tell part of the story, because they only count whether a tree has at least one trait measurement in TRY. To get decent estimates of the mean of a trait like leaf nitrogen content you need LOTS of replication, preferably >10,000 data points to account for all the bias that can be introduced by site, season, leaf age, tree age, leaf location on the tree, measurement error, etc.