I wanted to calculate the minimum bounding rectangle around various polygons in a dataset I was working on. The minimum bounding rectangle is the smallest rectangle that totally encompasses the given polygon.
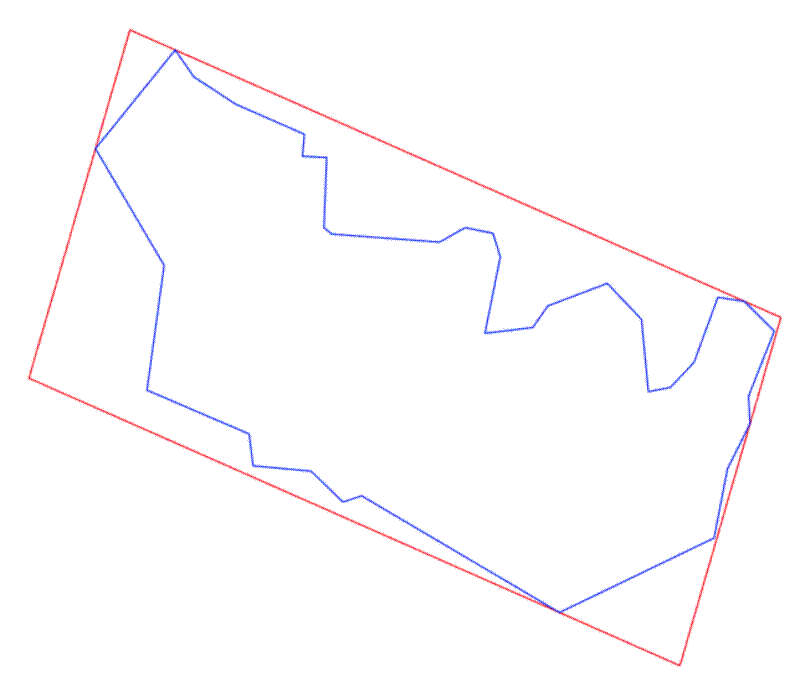
I have been using R and the sf package to work with the polygons. The polygons represent projected tree crown areas. The minimum bounding rectangle is a useful thing to calculate as it can tell you about elongation of the polygon and the direction of the axis of elongation, which in my case might tell me something about wind direction.
I wrote this function which returns the vertex point coordinates, width, length, and long-axis angle of the minimum bounding rectangle around a set of polygons:
#' Return the minimum bounding rectangle around a set of polygons
#'
#' @param x sf object containing only geometries of type \code{POLYGON} or
#' \code{MULTIPOLYGON}
#'
#' @return list containing vertex points (\code{ptx}),
#' width (\code{width}) length (\code{length}) and angle of bounding
#' rectangle of each polygon.
#'
#' @examples
#' dat <- sf::st_read(system.file("shape/nc.shp", package="sf"))
#' min_box_list <- minBox(dat)
#' min_box_list[[1]]
#'
#' min_box_sf <- do.call(rbind, lapply(min_box_list, function(x) {
#' pts_sf <- sf::st_as_sf(as.data.frame(x$pts), coords = c("X", "Y"))
#' sf::st_sf(geometry = sf::st_convex_hull(sf::st_union(pts_sf)), crs = sf::st_crs(dat))
#' }))
#' plot(sf::st_geometry(min_box_sf), col = NA, border = "red")
#' plot(sf::st_geometry(dat), col = NA, border = "blue", add = TRUE)
#'
#' @importFrom sf st_is st_coordinates
#'
#' @export
#'
minBox <- function(x) {
stopifnot(all(sf::st_is(x, c("POLYGON", "MULTIPOLYGON"))))
lapply(sf::st_geometry(x), function(y) {
x_mat <- sf::st_coordinates(y)[,1:2]
# Extract convex hull of polygon
H <- chull(x_mat)
n <- length(H)
hull <- x_mat[H, ]
# Get direction vector
hDir <- diff(rbind(hull, hull[1,]))
hLens <- sqrt(rowSums(hDir^2))
huDir <- diag(1/hLens) %*% hDir
ouDir <- cbind(-huDir[,2], huDir[,1])
# Project hull vertices
projMat <- rbind(huDir, ouDir) %*% t(hull)
# Get width and length of bounding rectangle
rangeH <- matrix(numeric(n*2), ncol = 2)
rangeO <- matrix(numeric(n*2), ncol = 2)
widths <- numeric(n)
lengths <- numeric(n)
for(i in seq(along=numeric(n))) {
rangeH[i,] <- range(projMat[i,])
rangeO[i,] <- range(projMat[n+i,])
widths[i] <- abs(diff(rangeH[i,]))
lengths[i] <- abs(diff(rangeO[i,]))
}
eMin <- which.min(widths*lengths)
hProj <- rbind(rangeH[eMin,], 0)
oProj <- rbind(0, rangeO[eMin,])
# Move projections to rectangle corners
hPts <- sweep(hProj, 1, oProj[,1], "+")
oPts <- sweep(hProj, 1, oProj[,2], "+")
# Get corner coordinates
basis <- cbind(huDir[eMin,], ouDir[eMin,])
hCorn <- basis %*% hPts
oCorn <- basis %*% oPts
pts <- t(cbind(hCorn, oCorn[,c(2,1)]))
# Angle
dPts <- diff(pts)
e <- dPts[which.max(rowSums(dPts^2)), ]
eUp <- e * sign(e[2])
deg <- atan2(eUp[2], eUp[1])*180/pi
return(list(pts = pts, length = lengths[eMin],
width = widths[eMin], angle = deg))
})
}
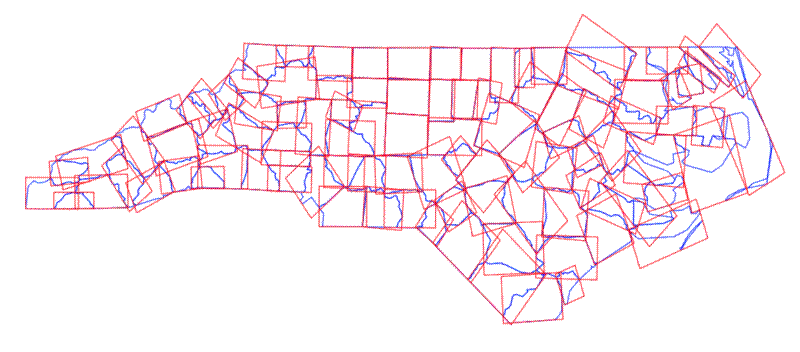
Here is the output of the example code in the function definition, showing the minimum bounding rectangles of each county in North Carolina, which is a dataset included in the sf package.