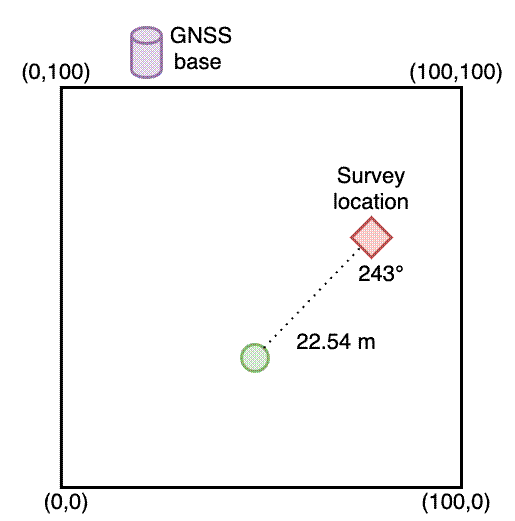
In 2018 and 2019 I set up some 100x100 m (1 ha) permanent vegetation monitoring plots in Bicuar National Park, southwest Angola. We measured the stem diameter of each tree stem >5 cm diameter and attached a numbered metal tag to each of these stems so we could track the growth and mortality of each stem over time. At the same time as measuring the stem diameters and attaching the tags, I also took a quick GPS point with a Garmin GPSMAP 65s Handheld GPS unit.
There are two main reasons to record the location of each stem in the plot. The first is to make it easier to relocate stems in the future. Sometimes tags fall off or stems are completely vaporised by fire. If we know the location of the stem, we can visit that location and confirm what has happened to the stem since the last survey. The second reason is that if we understand the spatial distribution of stems, we can better understand competitive (or facilitative) interactions among individuals, and look at how these interactions affect biomass dynamics.
When I revisited the plots in 2022, my goal was to collect lots of auxiliary data, to enrich our picture of the ecosystem. Alongside collecting data on woody debris, herbaceous biomass, and tree leaf traits, I also recorded the position of stems that had recruited since the initial survey back in 2018/2019. Instead of using a GPS, this time I used tape measures to record the position of each stem, using an XY coordinate system.
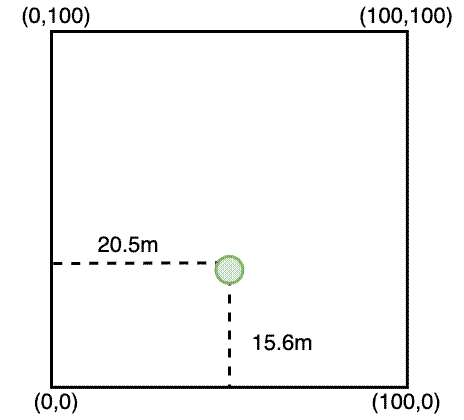
While we had the tape measures set up, I also re-recorded the positions of existing stems so I could compare the two methods of measuring the stem location. Others have encouraged me to use tape measures, suggesting that the GPS isn’t accurate enough, but tape measures takes a long time in the field compared to a GPS. If the accuracy of the GPS points is good enough, there’s no need to waste time with the tape measures.
To make the latitude-longitude coordinates comparable with the XY coordinates, I converted the lat-long coordinates to XY coordinates using a function I wrote in R. Hopefully the comments on the code suffice to describe what’s going on, but the basic idea is that the function takes a dataframe of stem measurements in multiple plots and an {sf} polygons object with multiple plot polygons, linked by the plot_id column. For each plot, the function follows this process:
- Find the southwest and southeast corners of the polygon
- Rotate both the polygon and the stem locations so that the SW-SE axis of the polygon runs exactly E-W.
- Calculate the E-W and N-S distance from the southwest corner of the plot to each stem location, in metres.
#' Convert lat-long stem coordinates to XY grid coordinates
#'
#' In rectangular plots to convert latitude and longitude coordinates to XY
#' grid coordinates, using the southwest corner of the plot as the origin point
#' (0,0), with the X axis increasing west -> east.
#'
#' @param x dataframe of stem data
#' @param polys sf object containing plot polygons, assumes all are rectangular
#' @param stem_plot_id column name string of plot IDs in x
#' @param polys_plot_id column name string of plot IDs in polys
#' @param longitude column name string of stem longitude in x
#' @param latitude column name string of stem latitude in x
#' @param x_crs coordinate reference system (CRS) or EPSG code of stem
#' coordinates.
#'
#' @return dataframe of measurement IDs with x_grid and y_grid filled
#' with estimated XY grid coordinates. NA values returned if
#' longitude and latitude were missing.
#'
#' @examples
#'
#'
#' @export
#'
gridCoordGen <- function(x, polys, stem_plot_id = "plot_id",
polys_plot_id = stem_plot_id, measurement_id = "measurement_id",
longitude = "longitude", latitude = "latitude",
x_crs = 4326) {
# Split stems by plot_id
x_split <- split(x, x[[stem_plot_id]])
# For each plot
grid_all <- do.call(rbind, lapply(seq_along(x_split), function(y) {
# Get plot ID
plot_id <- unique(x_split[[y]][[stem_plot_id]])
# Subset polys to plot ID
poly_fil <- polys[polys[[polys_plot_id]] == plot_id,]
# Convert corners to points
poly_points <- as.data.frame(sf::st_coordinates(poly_fil)[1:4,1:2])
# Get UTM zone of corners
utm_string <- UTMProj4(latLong2UTM(mean(poly_points[,1]), mean(poly_points[,2])))
# Convert polygons to UTM
poly_utm <- sf::st_transform(poly_fil, utm_string)
# Convert UTM polygons to points
points_utm <- sf::st_cast(poly_utm, "POINT", warn = FALSE)[1:4,]
# Extract coordinates as dataframe
coords_utm <- as.data.frame(sf::st_coordinates(points_utm)[1:4,1:2])
# Define points to match corners to
match_point <- sf::st_sfc(sf::st_point(
x = c(mean(coords_utm$X) - 1000, mean(coords_utm$Y) - 1000)))
other_point <- sf::st_sfc(sf::st_point(
x = c(mean(coords_utm$X) + 1000, mean(coords_utm$Y) - 1000)))
# Set CRS
sf::st_crs(other_point) <- utm_string
sf::st_crs(match_point) <- utm_string
# Get sw and se corner
sw_corner <- points_utm[sf::st_nearest_feature(match_point, points_utm),]
se_corner <- points_utm[sf::st_nearest_feature(other_point, points_utm),]
# Convert to WGS for geosphere compatibility
sw_wgs <- sf::st_coordinates(sf::st_transform(sw_corner, 4326))
se_wgs <- sf::st_coordinates(sf::st_transform(se_corner, 4326))
# Find rotation along SW,SE edge
xy_bearing <- geosphere::bearing(sw_wgs, se_wgs)
# Get centroid of polygon
cent <- sf::st_centroid(sf::st_geometry(poly_utm))
# Get location of sw corner
sw_cent <- sf::st_geometry(sw_corner)
# Convert angle to radians for rotation
angle <- NISTunits::NISTdegTOradian(90 - xy_bearing)
# Convert stem coords to sf object
x_sf <- st_as_sf(
x_split[[y]][,c(measurement_id, longitude, latitude)],
coords = c(longitude, latitude), na.fail = FALSE)
st_crs(x_sf) <- x_crs
# Transform stems sf to UTM
x_utm <- st_transform(x_sf, utm_string)
# Rotate the stems same as polygon
x_rot <- (sf::st_geometry(x_utm) - cent) * rot(angle) * 1 + cent
sw_cent_rot <- (sw_cent - cent) * rot(angle) * 1 + cent
st_crs(sw_cent_rot) <- st_crs(points_utm)
st_crs(x_rot) <- st_crs(points_utm)
x_cent <- x_rot - sw_cent_rot
x_cent_df <- as.data.frame(st_coordinates(x_cent))
names(x_cent_df) <- c("x_grid", "y_grid")
# Add cordinates to dataframe
x_out <- cbind(st_drop_geometry(x_sf), x_cent_df)
# Sub in empty stems
if (any(!x_split[[y]][[measurement_id]] %in% x_out[[measurement_id]])) {
missed_stems <- x_split[[y]][
!x_split[[y]][[measurement_id]] %in% x_out[[measurement_id]],
c(measurement_id)]
x_out <- rbind(x_out, missed_stems)
# NaN to NA
x_out$x_grid <- fillNA(x_out$x_grid)
x_out$y_grid <- fillNA(x_out$y_grid)
}
# Return
x_out
}))
# Return
return(grid_all)
}
I then matched the measurements using the tag ID of each stem, calculated the distance between them, and the angle between the tape measure and the GPS using this function:
# Define function to calculate angle of line, in radians
calcAngle <- function(x, y) {
dst_diff <- as.numeric(x - y)
return(atan2(dst_diff[1], dst_diff[2]) + pi)
}
First, here is a map where I laid all the location errors from each of the 11 plots on top of each other.

One really interesting thing about the plot above is that it looks like the errors get larger in the top part of the plot, and also that the errors on the X axis are larger than the errors on the Y axis.
In the field we always started collecting the XY coordinates from the SW (bottom-left) corner of the plot, doing 20 m lines of trees running E-W up to the NE corner. I wonder if the errors are larger at the top of the plot because we were getting tired towards the end of the day. Or maybe they were due to tape measure stretch? Also from this plot I get the impression that the errors are generally larger on the E-W axis than on the N-S axis. I’d expect the GPS to produce random errors, while the tape measures would produce systematic errors, so this plot suggests actually that there might be greater error in the tape measure coordinates than in the GPS.
Now here is a simple rose plot where I plotted all the lines with the tape measure position normalised to 0,0:
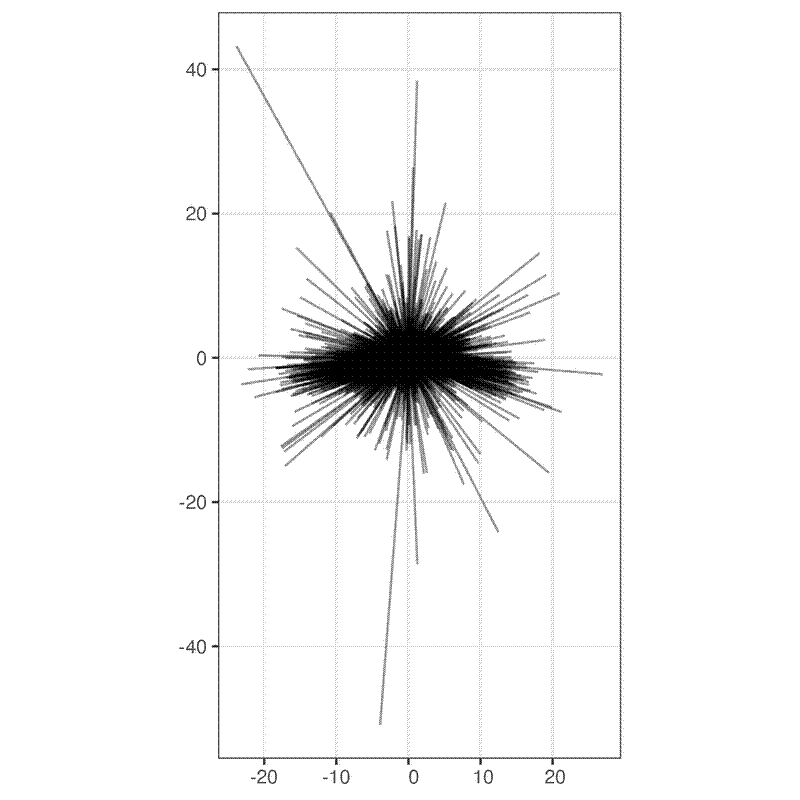
Again, this potentially shows that there’s greater error on the E-W axis. It also highlights some particularly large errors of >40 m, which I assume are reporting errors in the field.
And a histogram showing the distribution of error lengths:
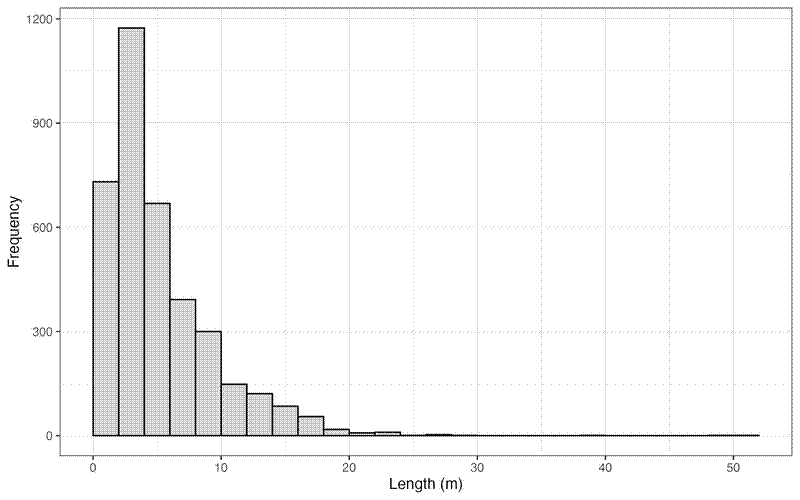
The mean error length was 5.2 m +/- 4.245 m SD, median = 3.9 m, with a range of 0.067 m to 51 m.
Next, I binned the error vectors by angle, into 20 degree bins, and calculated the sum of error lengths within each bin:
dat_length_bin <- dat_angle %>%
mutate(angle_bin = cut_width(angle_deg, 20, boundary = 0,
closed = "right")) %>%
group_by(angle_bin) %>%
summarise(
line_length_sum = sum(line_length)) %>%
mutate(angle_bin = as.numeric(gsub("\\[([0-9]+),.*", "\\1", angle_bin)))
Then plotted a rose diagram of these summary data:
ggplot() +
geom_bar(data = dat_length_bin,
aes(x = angle_bin, y = line_length_sum),
stat = "identity", colour = "black", fill = "darkgrey", width = 20,
position = position_nudge(x = 10)) +
coord_polar() +
scale_y_continuous(expand = c(0.1, 0)) +
scale_x_continuous(limits = c(0, 360), breaks = c(0, 90, 270, 360)) +
theme_bw() +
theme(
axis.text.y = element_blank(),
axis.ticks.y = element_blank())
labs(x = expression("Angle"~(degree)), y = "Total length (m)")
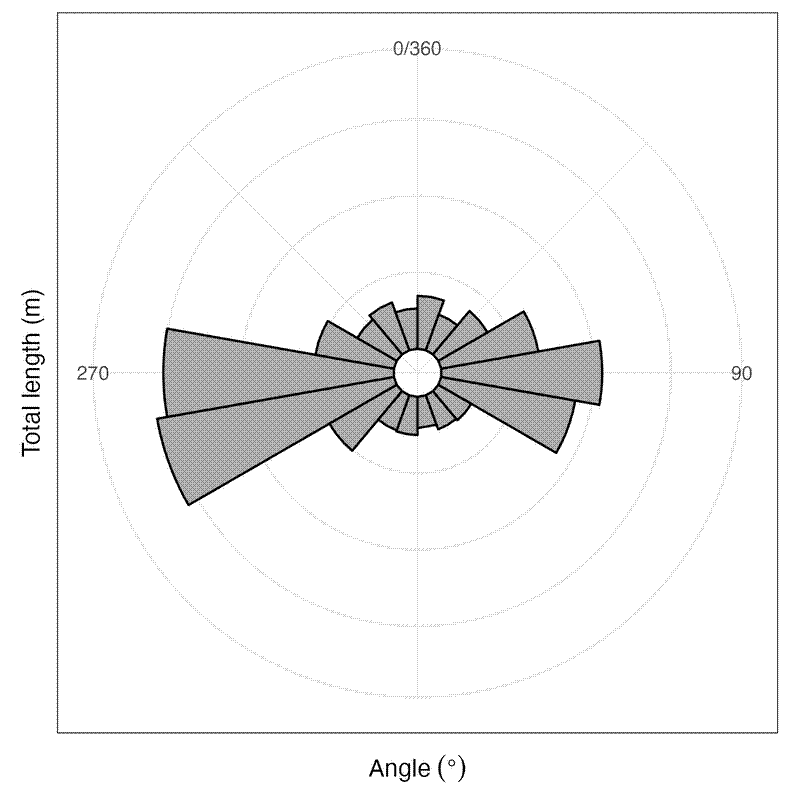
It looks like the biggest and most frequent errors are where the grid coordinate is west of the GPS coordinate. This systematic error probably has something to do with how we set up the tapes in the plots, and represents error in the grid coordinates rather than the GPS coordinates, as I’d expect the GPS coordinate error to be random noise. It suggests that the person measuring the X axis coordinate consistently over-estimated the position on the tape measure, likely because they weren’t holding the tapes perfectly perpendicular.
The main problem with this comparison between GPS and tape measure is that neither of these methods are guaranteed to provide the truth. There is random error in the GPS points, handheld GPS units are only accurate to about 2-3 m. However, there are also errors in the tape measure method:
Firstly, the edges of the plot might not be totally square. The XY coordinate system relies on the corners of the plot having a perfect 90 degree angle, and each edge being a perfectly straight line, but in the field this is difficult to achieve. Sometimes the plots come out slightly rhombic, despite our best efforts.
It’s also common for the tape measures to bow slightly in or out of the plot. If the edge bows in, the distance from the plot edge to a stem will be less in the middle of the plot than at the edges of the plot. This is a particularly problem in a grassy plot on a windy day, as the grass moves the tape measure. The only way to stop this is to place the tape measure very close to the ground and to anchor the tape measure at regular intervals.
The tape measures may stretch slightly leading to an under-estimate of the measurement.
The tape measures may not be laid out perfectly parallel to the plot edges. A tape measure laid out at an angle will increase the measured length. Using smaller strips along the X axis in the field, 10 m rather than 20 m, can reduce this error, as angle errors result in larger location erors with increased distance.
Finally, there may be reporting errors in the field, and there may be transcription errors when typing the data up onto the computer. Commonly decimal points are put in the wrong place, or 65.6 m gets called out as 45.6 m, when we move to a new row.
Where the goal is just to aid relocation of stems in future censuses, I would definitely advocate for using a GPS unit. It saves a lot of time, and the location accuracy is good enough. Where it’s necessary to quantify neighbourhood effects, I think tape measures can probably give better accuracy and higher precision, but only if the measuring is done by a trained team working meticuluously, and the plot is set up properly to begin with.
Another option for measuring tree location that I’ve been toying with for a long time is using a laser total station or a laser level in conjunction with differential GPS. Something like the Leica NA520 which can measure angle and distance to a reflective target. First you would pick a spot where many stems are visible and set up a survey tripod. Then using a differential GPS system you would record the precise location of the tripod. This could take a few minutes, but only has to be done once for each batch of measurements. Then the GPS antenna would be swapped out for a laser level. The distance and angle of each stem in view with respect to the level would be recorded. The survey tripod would be moved to the next surveying location and the process would be repeated. Then the location of each stem can be calculated using the real-space location of the survey tripod, the angle and distance of the stem with respect to the tripod. You could even record the same stem multiple times from different positions to further improve the accuracy of the location, but I think even for measuring neighbourhood effects it’s only really necessary to have an accuracy of about 50-100 cm.