John L. Godlee

In 2018 I wrote some code to convert stem locations within square plots from lat-long coordinates into XY grid coordinates. Recently I was asked to do the opposite, to convert XY grid coordinates into lat-long coordinates, so a colleague could combine multiple adjacent plots into one larger plot with a shared coordinate system. I’ve pasted the code for this procedure below:
# Convert XY grid coordinates to Lat-long coordinates
# John L. Godlee (johngodlee@gmail.com)
# Last updated: 2024-06-12

# Packages
library(dplyr)
library(sf)
library(NISTunits)
library(geosphere)
library(ggplot2)

# Define functions

#' Get valid UTM zone from latitude and longitude in WGS84 decimal degrees
#'
#' @param x vector of longitude coordinates in decimal degrees
#' @param y vector of latitude coordinate in decimal degrees
#'
#' @return Vector of UTM zones for each latitude-longitude pair
#' 
#' @export
#' 
latLong2UTM <- function(x, y) {
  unlist(lapply(1:length(x), function(z) {
    paste((floor((as.numeric(x[z]) + 180) / 6) %% 60) + 1,
      ifelse(as.numeric(y[z]) < 0, "S", "N"),
      sep = "")
  }))
}

#' Generate a valid UTM WGS84 proj4string given a UTM zone
#'
#' @param x character vector defining UTM zones
#'
#' @return UTM proj4string character vector
#' 
#' @export
#' 
UTMProj4 <- function(x){
  unlist(lapply(1:length(x), function(y) {
    paste0(
      "+proj=utm +zone=",
      gsub("[A-z]", "", as.character(x[y])),
      ifelse(gsub("[0-9]", "", as.character(x[y])) == "S", " +south", ""),
      " +ellps=WGS84")
  }))
}

#' Perform a rotation on an sf object
#'
#' @param a angle to rotate, in radians
#'
#' @keywords internal
#' @noRd
#' 
rot <- function(a) { 
  matrix(c(cos(a), sin(a), -sin(a), cos(a)), 2, 2) 
}

# Define UTM zone for test polygon location
utm_crs <- "+proj=utm +zone=33 +south +ellps=WGS84"

# Define origin corner (SW) of test polygon
orig <- c(479000, 8319000)

# Create dataframe of polygon corners (100x100 m)
poly_df <- data.frame(
  longitude = c(orig[1], orig[1], orig[1] + 100, orig[1] + 100, orig[1]),
  latitude = c(orig[2], orig[2] + 100, orig[2] + 100, orig[2], orig[2]))

# Convert dataframe of corners to a polygon
poly_ex <- st_convex_hull(summarise(st_as_sf(poly_df, 
      coords = c("longitude", "latitude"), crs = utm_crs)))

# Get the centroid of the polygon and rotate a bit
poly_ex_cent <- st_centroid(st_geometry(poly_ex))

rot_ex <- sample(seq(0, 360, 1), 1)

poly_ex_rot <- st_sf(geometry = (st_geometry(poly_ex) - poly_ex_cent) * 
  rot(NISTdegTOradian(rot_ex)) * 1 + poly_ex_cent)

st_crs(poly_ex_rot) <- utm_crs

# Transform rotated polygon to UTM
poly_ex_wgs <- st_transform(poly_ex_rot, 4326)
poly_ex_wgs$plot_id <- "A"

# Sample points within the rotated polygon
xy_range <- seq(0, 100, 0.5)
s_ex <- data.frame(
  plot_id = "A",
  x_grid = sample(xy_range, 50),
  y_grid = sample(xy_range, 50))

# Rename polygon and stem data to test code below.
poly_data <- poly_ex_wgs
x <- s_ex

# Add ID column
x$id <- seq_len(nrow(x))

# Get UTM zone of polygon centroid
poly_cent <- st_coordinates(st_centroid(poly_data))
utm_string <- UTMProj4(latLong2UTM(poly_cent[1], poly_cent[2]))

# Convert polygon to UTM
poly_utm <- st_transform(poly_data, utm_string)

# Convert UTM polygon to points
points_utm <- st_cast(poly_utm, "POINT", warn = FALSE)[1:4,]

# Extract coordinates as dataframe
coords_utm <- as.data.frame(st_coordinates(points_utm)[1:4,1:2])

# Define points to match corners to
match_point <- st_sfc(st_point(
    x = c(mean(coords_utm$X) - 1000, mean(coords_utm$Y) - 1000)))
other_point <- st_sfc(st_point(
    x = c(mean(coords_utm$X) + 1000, mean(coords_utm$Y) - 1000)))

# Set CRS
st_crs(other_point) <- utm_string
st_crs(match_point) <- utm_string

# Get sw and se corner
sw_corner <- points_utm[st_nearest_feature(match_point, points_utm),]
se_corner <- points_utm[st_nearest_feature(other_point, points_utm),]

# Convert to WGS for geosphere compatibility
sw_wgs <- st_coordinates(st_transform(sw_corner, 4326))
se_wgs <- st_coordinates(st_transform(se_corner, 4326))

# Find rotation along SW,SE edge
xy_bearing <- bearing(sw_wgs, se_wgs)

# Get centroid of polygon in UTM
cent <- suppressWarnings(st_centroid(st_geometry(poly_utm)))

# Get location of sw corner
sw_cent <- st_geometry(sw_corner)

# Convert angle to radians for rotation
angle <- NISTdegTOradian(90 - xy_bearing)

# Rotate polygon so SW-SE is flat
poly_rot <- (st_geometry(poly_utm) - cent) * rot(angle) * 1 + cent
st_crs(poly_rot) <- st_crs(poly_utm)

# Add SW UTM X and Y to XY grid coordinates
points_rot <- st_cast(poly_rot, "POINT", warn = FALSE)[1:4]
sw_corner_rot <- points_rot[st_nearest_feature(match_point, points_rot)]
se_corner_rot <- points_rot[st_nearest_feature(other_point, points_rot)]
x$x_grid_utm <- x$x_grid + st_coordinates(sw_corner_rot)[1]
x$y_grid_utm <- x$y_grid + st_coordinates(sw_corner_rot)[2]

x_sf <- st_as_sf(
  x[,c("id", "x_grid_utm", "y_grid_utm")], 
  coords = c("x_grid_utm", "y_grid_utm"), 
  na.fail = FALSE, crs = st_crs(poly_rot))

# Rotate coordinates back
x_sf_rot <- (st_geometry(x_sf) - cent) * rot(-angle) * 1 + cent
st_crs(x_sf_rot) <- st_crs(x_sf)

# Transform stems to WGS84
x_wgs <- st_transform(x_sf_rot, 4326)
x_out <- as.data.frame(cbind(x$id, st_coordinates(x_wgs)))
names(x_out) <- c("id", "longitude", "latitude")

# Clean dataframe
out <- x_out[order(x_out$id),c("longitude", "latitude")]
out$id <- NULL

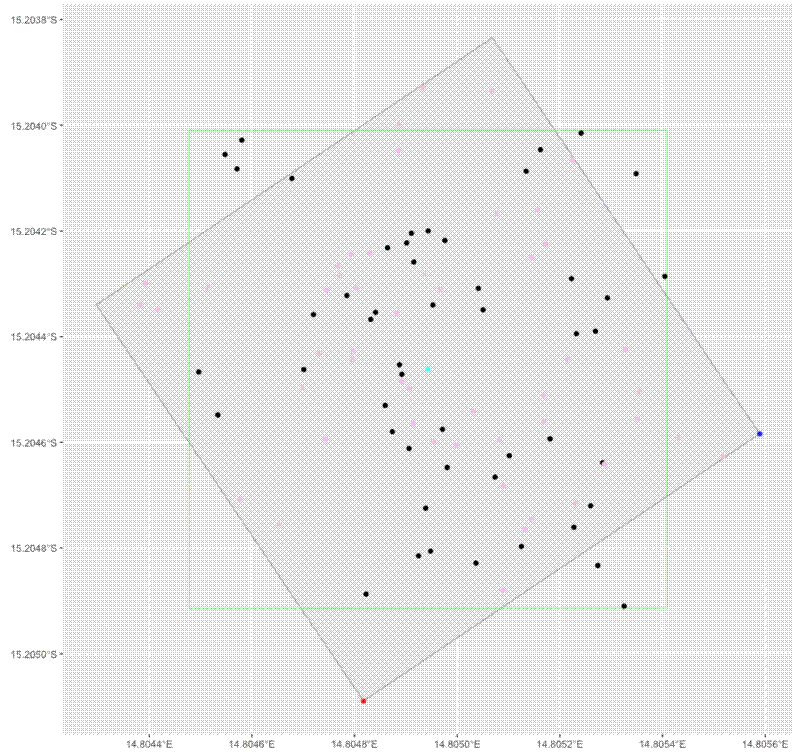
# Create plot to illustrate code above
ggplot() +
 geom_sf(data = poly_utm) +
 geom_sf(data = sw_corner, colour = "red") +
 geom_sf(data = se_corner, colour = "blue") +
 geom_sf(data = cent, colour = "cyan") + 
 geom_sf(data = poly_rot, colour = "green", fill = NA) + 
 geom_sf(data = x_sf) + 
 geom_sf(data = x_sf_rot, colour = "pink") 

# This dataframe contains lat-long coordinates for each row of x
out
Demonstration of the code to converrt lat-long coordinates to XY coordinates.
Converting stem locations from lat-long to XY coordinates

2024-06-12
